Hoja de Ejercicios de Apoyo para los temas 1 y 2.

Tema 1 (Números Reales) y Tema 2 (Polinomios)

Conceptos fundamentales Tema 1: Números Reales:

• Números Naturales (N): Los positivos
• Números Enteros (Z): Los positivos, los negativos y el 0.
• Números Racionales (Q): Los enteros, las fracciones y aquellos decimales que pueden convertirse en fracción: (decimales exactos, decimales periódico puros y decimales periódico mixtos).
• Los números Irracionales (I): Los decimales que no pueden convertirse en fracción, las raíces no exactas y algunos números como e, pi …
• Conversión de decimal a fracción (Fracción Genetratriz):
• Decimal exacto: Se divide al número sin comas por un 1 seguido de tantos 0 como cifras decimales haya.
• Decimal periódico puro: Se divide al número sin comas menos la parte no periódica sin comas por tantos 9 como cifras de periodo haya.
• Decimal periódico mixto: Se divide al número sin comas menos la parte no periódica sin comas por tantos 9 como cifras de periodo haya seguido de tantos 0 como cifras de anteperiodo haya.

• Aproximaciones:
• Aproximación Por Exceso: Consiste en añadir una cifra mas a la última anterior al corte
• Aproximación Por defecto ó truncamiento : Consiste en dejar el número como está al cortar en la cifra pedida.
• Aproximación por Redondeo: Consiste en áñadir una número mas a la última cifra si ésta es 5 ó superior y dejarlo como está sino llega a 5.

• Errores:
• Errores de una aproximación: Error Absoluto:  Indica una cantidad de error. Es el valor absoluto de la resta del valor exacto menos el valor aproximado.
• Errores de una aproximación: Error Relativo: Indica una proporción de error. Es el cociente entre el error absoluto y el valor exacto.
• Representaciones en la Recta Real:
• Representación de números racionales (fracción propia) en la recta real: Es una aplicación del teorema de Tales: Trazamos una recta oblicua desde el 0 y la dividimos en tantas partes como sea el denominador, unimos el extremo con el 1 y hacemos paralelas, marcamos donde corta la paralela del número del numerador.
• Representación de números racionales (fracción impropia) en la recta real: Es una aplicación del teorema de Tales: En primer lugar dividimos el numerador entre el numerador obteniendo un cociente y un resto. Trazamos una recta oblicua desde el Cociente y la dividimos en tantas partes como sea el denominador, unimos el extremo con el Cociente +1 y hacemos paralelas, marcamos donde corta la paralela del número del resto.
• Representación en la recta real de raices no-exactas: Es una aplicación del teorema de Pitágoras que consiste en buscar dos números elevados al cuadrado que nos dé el número del radicando que queremos representar, esos dos números serán los catetos de un triángulo rectángulo que situaremos en la recta real, finalmente desplazamos la hipotenusa con un compás sobre la recta real.

• Intervalos: Segmentos sobre la recta real, que podrán ser abiertos (si no se incluyen los extremos), cerrados (si incluiremos los extremos) y semiabiertos por la izquierda ó derecha (según cual de los dos extremos es el que no icluimos).
• Semirrectas: Intervalos donde uno de los dos extremos es siempre un infinito y el otro podrá ser abierto (no incluido) ó cerrado (incluido).
• Entornos: E(Centro, Radio).
• Convertir los entornos en intervalos:

Extremo inferior del intervalo=Centro-Radio

Extremo superior del intervalo=Centro+Radio

• Convertir los intervalos en entornos:

Centro=(extremo inferior del intervalo+extremo superior del intervalo):2

Radio= extremo superior del intervalo-centro

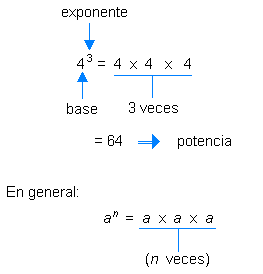
• Propiedades de las potencias (misma base, mismo exponente, potencia de potencia).

• Notación científica: Es una aplicación de las potencias para poder expresar y operar cantidades muy grandes ó muy pequeñas que consiste en expresar un número entre 1 y 9 seguido de una coma y decimales (si los hay) multiplicados por una potencia de base 10 y exponente el que corresponda. 

• Sumas y restas en notación científica: Antes debemos de poner ambos con la misma potencia de base 10

• Multiplicaciones y divisiones: Operamos la parte numérica por un lado y la parte de las potencias de 10 por otra.

• Radicales en función del índice y el radicando. (Potencias de exponente fraccionario)

• Propiedades de los radicales:
  

• Potencias de exponente negativo:

• Operaciones con raíces:
  

  ·         Propiedades de la raíces:  Sumas y Restas: Primero hay que extraer todos los factores posibles fuera del radical y despues operar sólo aquellos que tengan el mismo índice y el mismo exponente.

  ·         Propiedades de la raíces:  Multiplicación y División: Hay que hacer el mínimo común múltiplo de los índices y despues dividir éste por los índices originales, elevando el radicando al resultado.
• Radicales semejantes: Aquellos que tienen el mismo índice y el mismo radicando.

• Racionalización: consiste en eliminar las raíces de los denominadores para facilitar operaciones posteriores.

• Logaritmo: Base, Argumento. Definición, Propiedades.

 

• No existen los logaritmos de 0 ni de números negativos.
• Cambio de base:

•  Paso de expresión algebraica a logarítmica y viceversa: Consiste en aplicar las propiedades de los logaritmos:
• Ejemplo: Si el log x = a y el log y = b:

•  Aplicación de los logaritmos: Interés Compuesto:

Conceptos fundamentales Tema 2: Polinomios.

• Expresión algebraica: Es cualquier combinación de números y letras relacionados entre si por las operaciones aritméticas.
• Valor numérico de una expresión algebraica: Es el número que se obtiene al sustituir en ella las variables por números y realizar las operaciones.
• Monomio: Es una expresión algebraica formada por el producto de un número real y una ó mas variables elevadas a exponentes naturales.
• Polinomio: Es la suma de varios monomios.
• Grado de un monomio: La suma de los exponentes de sus variables.
• Grado de un polinomio: El del monomio de mayor grado que contenga.
• Suma y diferencia de polinomios: Se suman ó restan los monomios semejantes y se deja indicada la operación con los no-semejantes.
• Producto ó multiplicación de polinomios: Se multiplica cada monomio del primero por cada monomio del segundo, y luego se suman los términos semejantes.
• Potencia de un polinomio: Se multiplica el polinomio por si mismo tantas veces como lo indique el exponente.

• Identidades notables:

• División de polinomios (método tradicional, Regla de Ruffini):

• Teorema del resto y del factor:

• Raíces de un polinomio, factorización:

• Ejemplos de factorización:

Hoja de Ejercicios de los Temas 1 y 2:

¿Quien inventó la regla de Ruffini?

Está bastante claro: un matemático y médico italiano llamado Paolo Ruffini (1765-1822).
Durante su época de catedrático de matemáticas en Módena inventó su algoritmo para dividir polinomios siempre que el divisor fuera de primer grado y dió las claves para factorizar polinomios y hallar las raíces exactas de los polinomios.

No llevó nada bien la invasión del norte de Italia por parte de Napoleón, al que no juró lealtad, tuvo que abandonar su cátedra y trabajó de médico hasta la caída de Napoleón, entonces no solo recuperó la cátedra sino que llegó a ser el Rector de la universidad de Módena, una pena que pocos años despues tratando a sus pacientes de tifus se infectó y acabó muriendo por esta enfermedad, aunque poco antes de su muerte tuvo el humor de escribir un libro sobre su experiencia con el tifus bastante valioso desde el punto de vista médico.

Éste es el aspecto que tenía Paolo Ruffini:

¿Quien inventó los logaritmos?

Fue un matemático, físico, astrónomo y teólogo escoces llamado John Napier (1550-1617), además de todo ésto era el barón de Merchiston, pero fue conocido por todos como Neper, el inventor de los logaritmos, a los que llamaba números artificiales. Durante muchos años se dedicó a estudiar el apocalipsis y predijo el fin del mundo alrededor del año 1700, por aquella época llevaba mas de ochenta años muerto y no pudo percatarse de su error.

Éste es el aspecto que tenía John Neper: