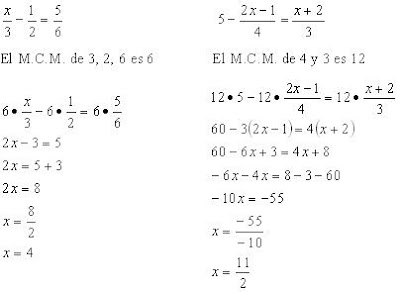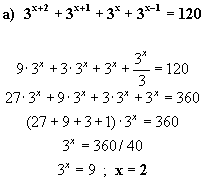1) Ecuaciones Polinómicas de Primer Grado:
Son aquellas formadas por polinomios donde la incógnita solo lleva exponente 1:
Seguimos la jerarquía habitual de operaciones: Paréntesis, Común denominador y finalmente las incógnitas a un lado y los números independientes al otro:
2) Ecuaciones Polinómicas de 2º Grado:
Son aquellas en las que el mayor exponente de las incógnitas es 2:
Hay algunas de segundo grado en las que se nos simplifican los términos de grado 2 y llegamos a ecuaciones de primer grado.
Las que sean completas se resuelven por la fórmula y las incompletas tambien pueden si sustituimos por 0 el término que falte.
Fórmula para las completas:
Aunque las incompletas tambien tienen otros métodos mas simples y rápidos:
De otra forma:
3) Ecuaciones polinómicas de Grado superior a 2:
Son aquellas en las que los exponentes de las incógnitas superan el grado 2.
Se resuelven por los métodos tradicionales de factorización de polinomios:
- Sacar factor común si se puede
- Aplicación de productos notables
- Regla de Ruffini
4) Ecuaciones Bicuadradas:
Sólo aparecen los terminos de exponente 4, exponente 2 y término independiente. (aunque pueden ser otros terminos, siempre que el exponente del mayor sea el doble que el del menor).
Se resuelven haciendo un cambio de variable:
Ejercicios propuestos:
5) Ecuaciones Racionales:
Son aquellas ecuaciones en las que tenemos incógnitas en los denominadores.
Se trata de eliminar los denominadores, para ello hay que hacer el mínimo común múltiplo entre ellos, despues dividiremos entre los denominadores originales y multiplicaremos por el numerador, simplificamos los denominadores a ambos lados y resolvemos la ecuación polinómica resultante.
Ejercicios Propuestos:
6) Ecuaciones Radicales:
Son aquellas en las que aparece la incógnita dentro de una raíz. Se resuelven aislando la raíz (dejándola sola a un lado de la igualdad), y elevando ambos miembros al cuadrado. Si aún así quedan raíces con incógnitas en el radicando repetiremos el proceso las veces que haga falta.
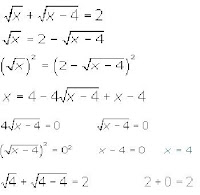


7) Ecuaciones Exponenciales:
Son aquellas en las que encontramos la incógnita en el exponente, se resuelven tratando de comparar bases ó exponentes y eliminando una de los dos, salvo aquellas en las que aparecen una base elevada a la incógnita y tambien la misma base elevada al doble de la incógnita, en estas el cambio de variable es imprescindible.
Ejercicios Propuestos:
8) Ecuaciones Logarítmicas:
Son aquellas ecuaciones en las que encontramos logaritmos de expresiones algebraícas. El método mas habitual de resolución es aplicar propiedades de los logaritmos hasta que tengamos un único logaritmo de cada miembro, entonces podremos quitarlos y resolver la ecuación algebraíca que quede.